この記事について
この記事では、「Web上で3D表示作って遊びたい」という人向け、三次元表示の方法と基本的な考え方をまとめたものです。
JavaScriptとp5.jsという簡単にお絵かきができるライブラリを用いて説明します。気軽に読んでください。
p5.jsを使おう
今回、画面に絵を描くためのライブラリとしてp5.jsを使います。これは○とか■などの図形描画を簡単に命令で書くためのライブラリなのですが、なんと2D表示だけでなく3D表示もできます。
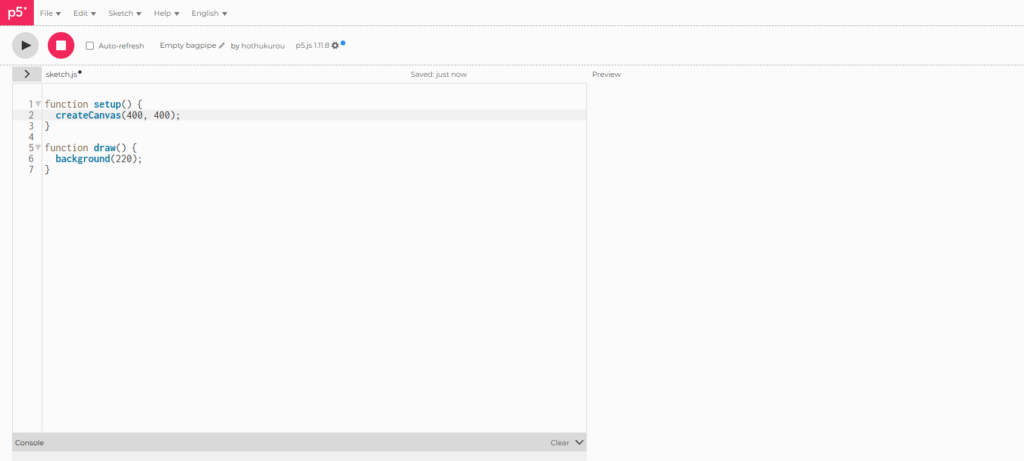
p5.jsを使うためには、htmlというWebページを作成したりp5.jsのライブラリを読み込ませるコードを書いたりする必要があるのですが、めんどうなのでここではWeb上で動作を確認できるエディタを使いましょう。
・p5.js WebEditor
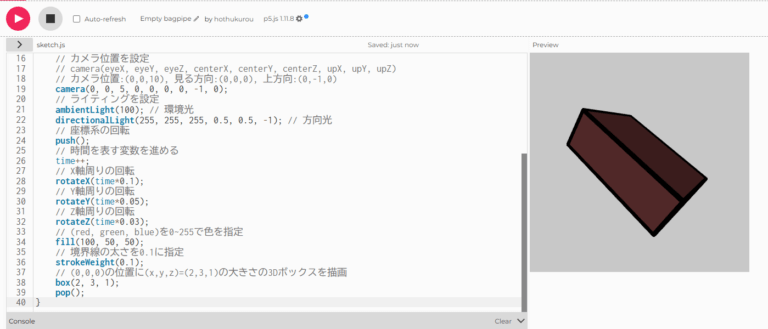
以下のような画面が開けばOKです。
3Dのboxを書こう
さて、早速プログラムしましょう。まずは画面中央に箱を表示するコードです。
画面左側のコード欄に以下をコピペして貼ってみてください。
function setup() {
const screenWidth = 400;
const screenHeight = 400;
// 3Dレンダラーを使用してキャンバスを作成
createCanvas(screenWidth, screenHeight, WEBGL);
// フレームレートを設定
frameRate(30);
// 画角(Field of View)を設定:PI/3 = 60度 screenWidth / screenHeight:横/縦の画面比 0.1:Near 100:far
perspective(PI / 3, screenWidth / screenHeight, 0.1, 100);
}
let time = 0;
function draw() {
// 背景色を設定
background(200);
// カメラ位置を設定
// camera(eyeX, eyeY, eyeZ, centerX, centerY, centerZ, upX, upY, upZ)
// カメラ位置:(0,0,10), 見る方向:(0,0,0), 上方向:(0,1,0)
camera(0, 0, 5, 0, 0, 0, 0, 1, 0);
// ライティングを設定
ambientLight(100); // 環境光
directionalLight(255, 255, 255, 0.5, 0.5, -1); // 方向光
// 座標系の回転
push();
// 時間を表す変数を進める
time++;
// X軸周りの回転
rotateX(time*0.1);
// Y軸周りの回転
rotateY(time*0.05);
// Z軸周りの回転
rotateZ(time*0.03);
// (red, green, blue)を0~255で色を指定
fill(100, 50, 50);
// 境界線の太さを0.1に指定
strokeWeight(0.1);
// (0,0,0)の位置に(x,y,z)=(2,3,1)の大きさの3Dボックスを描画
box(2, 3, 1);
pop();
}
設定後、以下の▶ボタンを押すと、右側に四角形が表示されると思います。

起動するとBoxが回転した映像が画面右に映ります。
グルグル回りますね。これを例に三次元描画の仕組みを見ていきましょう。
p5.jsのプログラムの仕組み
ここで今回3D描画ライブラリとして使っているp5.jsの使い方を説明します。
このライブラリは、以下の関数を指定のタイミングで実行します。
// プログラム起動時に一回だけ実施する関数
// ここにキャンバスの大きさやカメラの画角情報を書いていく
function setup(){
}
// 毎フレーム実行する関数
// ここに描画対象の定義やカメラ位置などを書いていく
function draw(){
}
setup関数では、キャンバスの大きさを指定します。今回は縦横400pxのキャンバスを表示しています。また、フレームレートはこの関数の中で設定します。
draw関数はフレームレートで指定した速さで呼ばれ続けます。フレームレートが30ならば、1秒間に30回呼ばれることになります。
draw関数の最初にbrackgroundという関数を呼んでいますが、これは「引数のグレースケールでキャンバスを塗りつぶす」処理で、画面の初期化に使います。
毎フレームごとに指定の色で塗りつぶして、その上で回転したBoxを表示していることで、アニメーションを表示しています。試しにbackground関数を消して実行すると、以下のように毎フレームごとに残像のように見えるBoxが見えるはずです。
これを消すために毎回background関数で塗りつぶしているのです。

毎回指定した色で塗りつぶすことで、前回の描画を消して書き直しているわけです。
では、次にこの箱の描画プログラムについて解説していきます。
三次元座標系を理解しよう
先ほどのプログラムはぐるぐると3Dが動くプログラムですが、動いている例だと説明が大変なので、まず箱が止まっている時のコードを解説します。以下のコードをコピペしてください。
function setup() {
const screenWidth = 400;
const screenHeight = 400;
// 3Dレンダラーを使用してキャンバスを作成
createCanvas(screenWidth, screenHeight, WEBGL);
// フレームレートを設定
frameRate(30);
// 画角(Field of View)を設定:PI/3 = 60度 screenWidth / screenHeight:横/縦の画面比 0.1:Near 100:far
perspective(PI / 3, screenWidth / screenHeight, 0.1, 100);
}
let time = 0;
function draw() {
// 背景色を設定
background(200);
// カメラ位置を設定
// camera(eyeX, eyeY, eyeZ, centerX, centerY, centerZ, upX, upY, upZ)
// カメラ位置:(0,0,10), 見る方向:(0,0,0), 上方向:(0,1,0)
camera(0, 0, 5, 0, 0, 0, 0, 1, 0);
// ライティングを設定
ambientLight(100); // 環境光
directionalLight(255, 255, 255, 0.5, 0.5, -1); // 方向光
// (red, green, blue)を0~255で色を指定
fill(100, 50, 50);
// 境界線の太さを0.1に指定
strokeWeight(0.1);
// (0,0,0)の位置に(x,y,z)=(2,3,1)の大きさの3Dボックスを描画
box(2, 3, 1);
}
以下のように静止した縦に長い長方形の画像が描画されるはずです。これを用いて解説していきます。
まずは2次元の話からしていきましょう。私たちは普段三次元の世界を二次元画像としてみているので、これをベースで話すとわかりやすいのです。
普段画像を使っているとき、左上を(x,y)=(0,0)とした以下のような座標系で画像を保存しています。
右が+X方向で、下が+Y方向です。
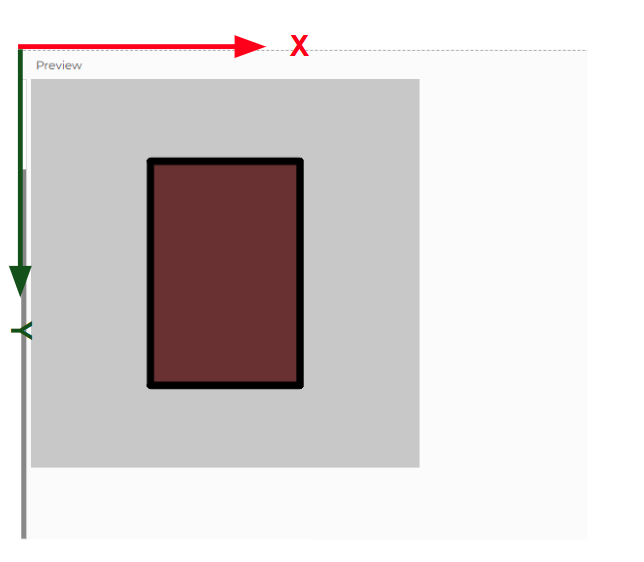
3次元座標を考える時は、これにZ軸を追加して奥行を持たせます。
Z軸の定義は2パターン考えられます。
奥方向を+Zとするか、手前方向を+Zにするかです。
これは3D描画ツールによって定義がまちまちなのですが、p5.jsでは手前側を+Z軸とします。
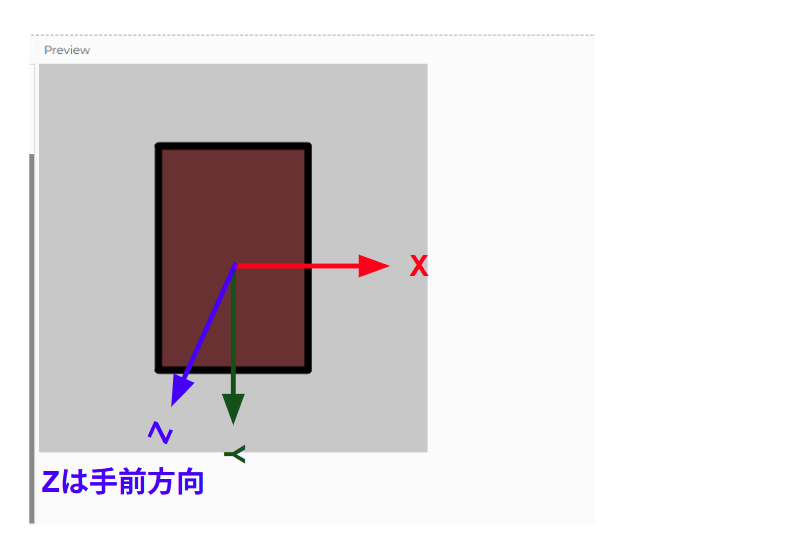
このようなZ軸の定義を左手座標系と呼びます。なぜ左手座標系と呼ぶかですが、左手の親指を+X軸、人差し指を+Y軸、中指を+Z軸とみるとこの座標系になるからです。
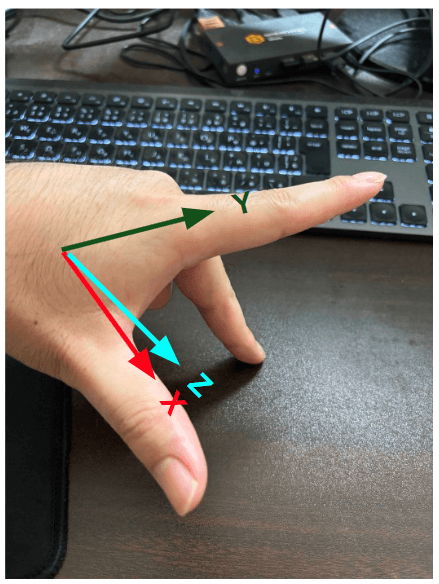
逆に、元の座標系でZ軸を奥側と定義した時の座標系を右手座標系と呼びます。これは右手で同じように指を伸ばすと同じ座標軸を確認できます。
今後3次元座標系の中で動作を考える時は、左手をこのような座標系の手にしてぐるんぐるんと目の前で動かしていくことになります。人間の認識は三次元理解に追いつかないので、実際に左手を動かして確認するんですね。
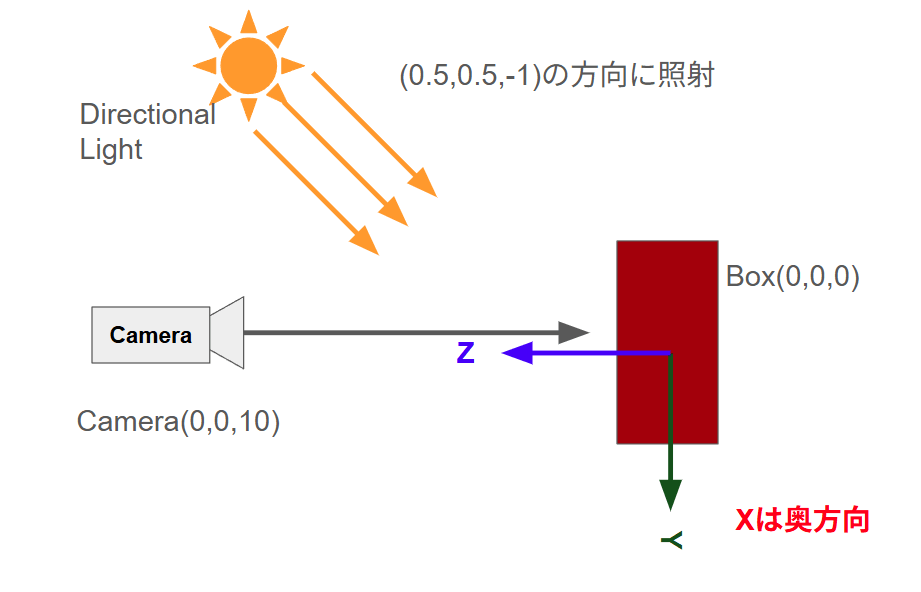
カメラとBoxの関係を理解しよう
今回書いたプログラムでは、カメラの位置、視線とBoxの位置とサイズを指定しています。
これを図にしたものが以下となります。
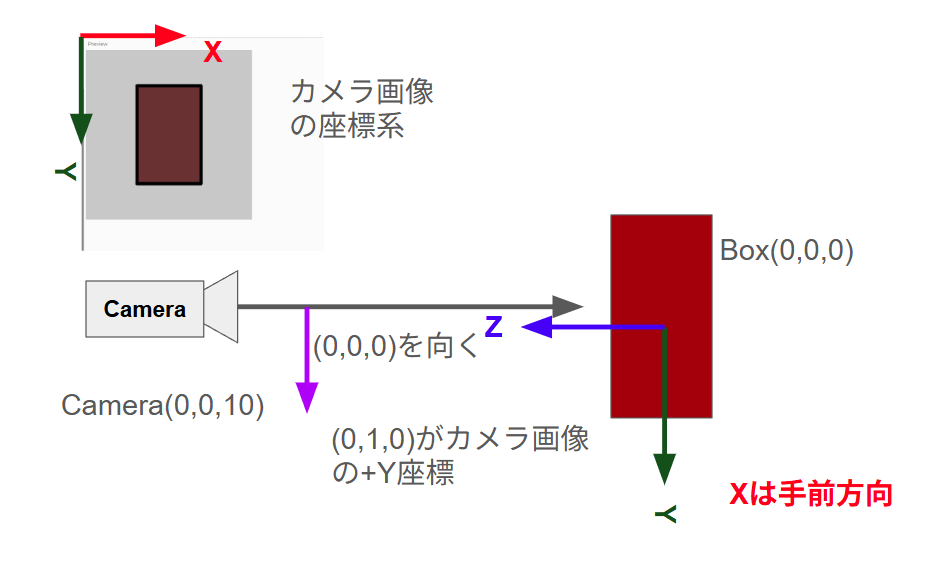
上の座標系をもとにカメラに映る画像を見ると先ほどの画像になります。
キャンバスに映った四角形は三次元空間内でカメラが撮影したはこの画像となります。

このような見え方になる原理を解説します。
一番簡単なBoxから説明しましょう。以下のコードの通り、色を指定してboxの引数にサイズを入れています。
y方向がx方向よりも長い形になっています。ちなみにBoxは中心を基準に表示されることに注意してください。
// (red, green, blue)を0~255で色を指定
fill(100, 50, 50);
// 境界線の太さを0.1に指定
strokeWeight(0.1);
// (0,0,0)の位置に(x,y,z)=(2,3,1)3Dボックスを描画
box(2, 3, 1);
ここまでは直感的ですが、カメラの定義をするとかなり混乱すると思いますのでなんとかしがみついてください。
三次元空間内にカメラを定義する時は以下のパラメータを決める必要があります。
・カメラ位置(eyeX~Z)
カメラがいる場所です。現実のカメラは大きさを持ちますが、データ上では点として定義されます。
・視線の1点(centerX~Z)
カメラが見ている視線の先の一点です。カメラ位置と視線の1点を結んだベクトルが視線の中央ベクトルとなります。
以下の図だと(0,0,10)から(0,0,0)を結ぶベクトルが視線の中央ベクトルになります。
Boxの中央が(0,0,0)の座標値なので、キャンバス中央が(0,0,0)となります。
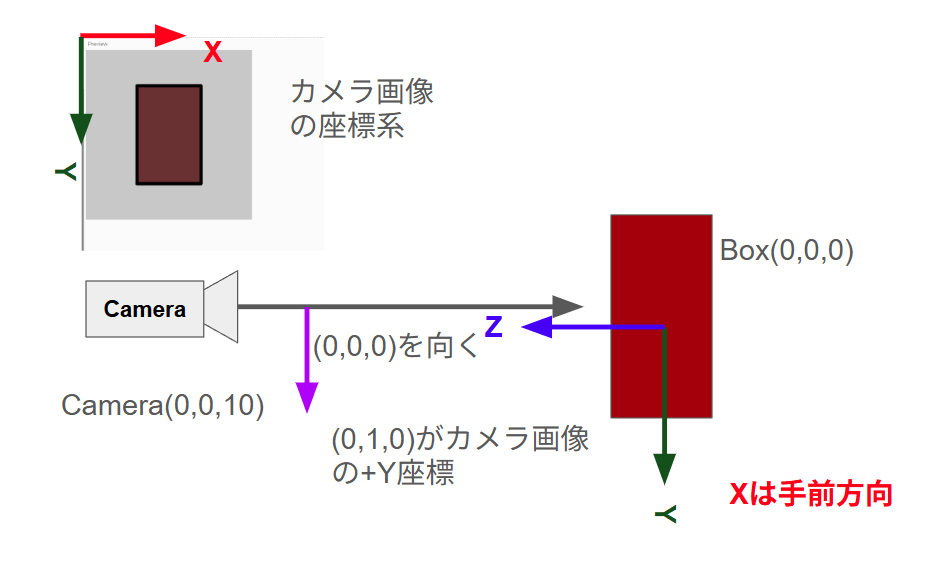
・画像の上の定義(upX~Z)
視線ベクトルだけではカメラが撮影する画像の定義はできません。視線ベクトルを軸にグルグルと回る自由度が残っているからです。これを決めないと、以下画像のように視線ベクトルを中心にぐるぐる回る画像のどれが正解か決めることができません。


そこで、カメラが撮影したカメラ画像のY軸方向がどの方向であるかを定義する必要があります。
upX~Zという名称からつい画像の上方向の定義であると考えてしまいますが、そうではない点に注意です。
カメラ画像の+Y軸の方向は三次元空間でどこを向いているのかという定義です。
カメラ画像の+Y軸は下を向いているので、この下方向のベクトルは三次元でどこを向いているのかを指示します。ものすごく紛らわしい話なので、いま一度下の画像を見て頭に叩き込みましょう。
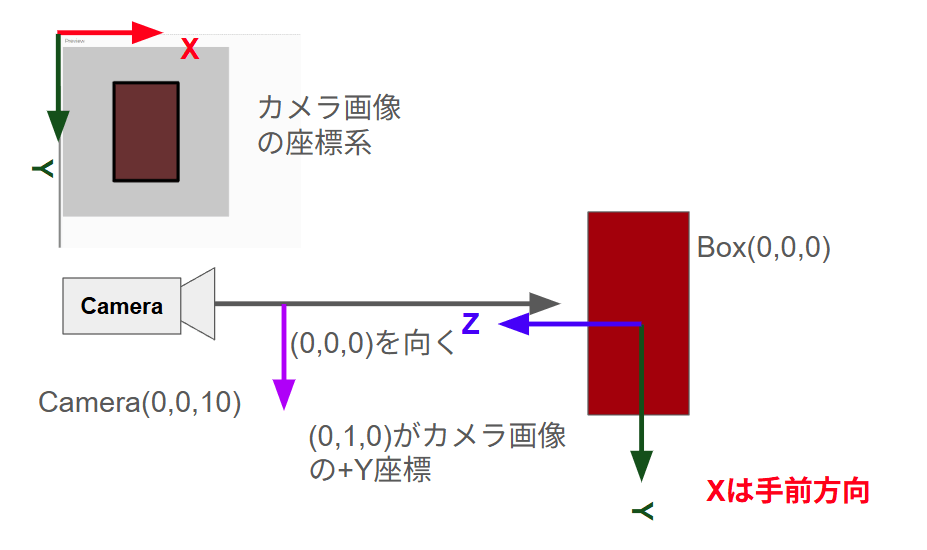
このupX~Zは視線ベクトルと垂直なベクトルで定義します。もし平行に設定するとキャンバスには何も映らなくなります。
この三点のパラメータを記入することではじめてカメラの画像をキャンバスに表示することができます。
具体的なコードは以下となります。
// カメラ位置を設定
// camera(eyeX, eyeY, eyeZ, centerX, centerY, centerZ, upX, upY, upZ)
// カメラ位置:(0,0,10), 見る方向:(0,0,0), 上方向:(0,1,0)
camera(0, 0, 5, 0, 0, 0, 0, 1, 0);
これでカメラの設定はできました。ただ、カメラの設定はこれだけではなくてsetup関数でカメラの画角や縦横比を定義する必要があります。
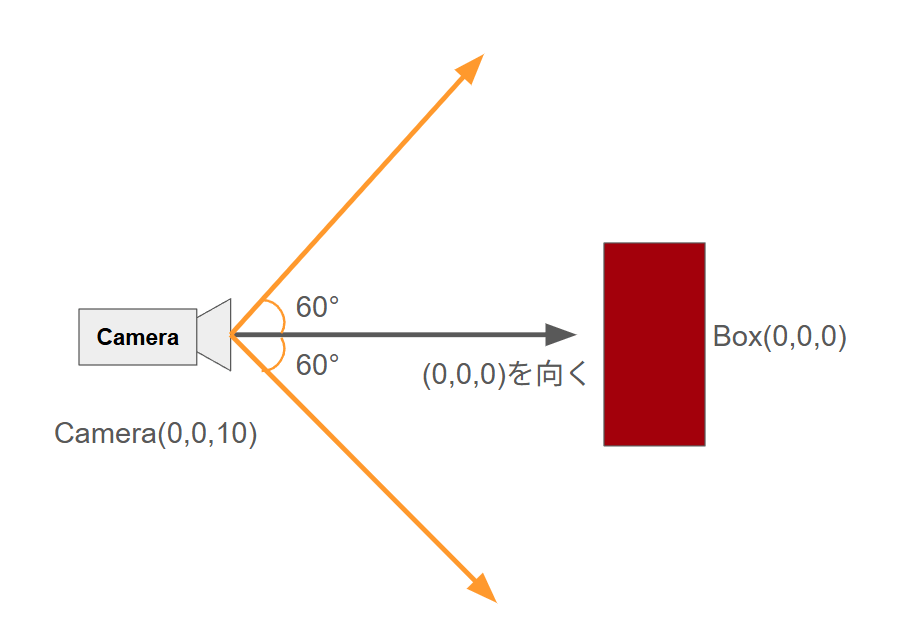
この画角は縦方向の画角です。また、視線の中央ベクトルからの広がりなので、以下のように倍の角度を見渡していることになります。
今回は縦の画角60度で設定しました。以下のようになります。
横の画角は、縦の画角を縦横比で掛け算した値で決まります。
今回は横も縦も同じ幅で定義しているので縦横比は1となり、横画角も同じ60度となります。
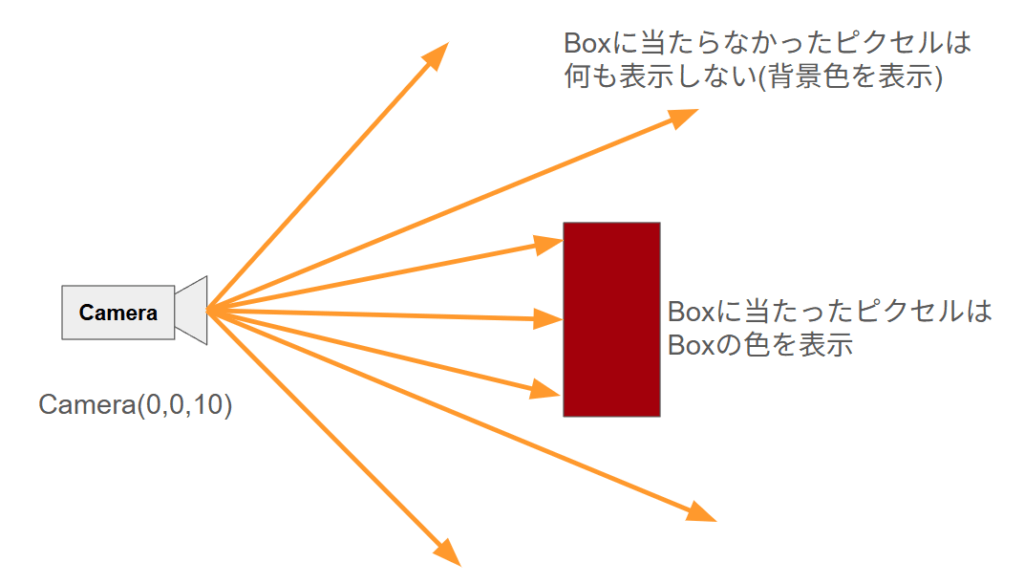
今回キャンバスのピクセルは縦横400pxなので、上記の120°の中を等角度でピクセルごとに視線ベクトルが飛んでいき、当たった物体の色を調べて、その色をピクセルの色とします。
400×400=160000本のピクセルごとのベクトルが飛んでいき、Boxに当たればその色が表示され、当たらなければ背景色が表示されます。
16万本というのはかなり大きな量ですが、PCに入っているGPUというパーツはこのような計算を大量に並列で実行できるので、30フレームでも計算ができてしまいます。GPUすごい!
このようなベクトルを飛ばしたときに「色判定を行う最小の距離(near)と最大の距離(far)」を指定して、この範囲でぶつかった場所を判定します。
今回はnearは0.1、farは100と設定しました。
このような設定を以下の項目で行っています。
// 画角(Field of View)を設定:PI/3 = 60度 screenWidth / screenHeight:横/縦の画面比
perspective(PI / 3, screenWidth / screenHeight, 0.1, 100);
光の設定を確認しよう
暗闇の中でBoxを見ても、黒色としか確認できません。光があることで、Boxの色を確認することができます。
光は色々な種類がありますが、ここではDirectional Light(直射光)とambientLight(環境光)を説明します。
Directional Lightは平行な光であり、光の色成分を第一引数から第三引数まで設定した後、光ベクトルを第四引数から第六引数まで設定します。今回は以下のような図で光を与えました。
ambientLightは方向を持たない光で、「角度関係なくまんべんなく明るい」を再現することができます。
// ライティングを設定
ambientLight(100); // 環境光
directionalLight(255, 255, 255, 0.5, 0.5, -1); // 方向光
Boxを回転させたり、移動させよう
ここからは、回転や移動の方法を解説する。改めて以下のコードをコピーして、その動作を確認してみましょう。
function setup() {
const screenWidth = 400;
const screenHeight = 400;
// 3Dレンダラーを使用してキャンバスを作成
createCanvas(screenWidth, screenHeight, WEBGL);
// フレームレートを設定
frameRate(30);
// 画角(Field of View)を設定:PI/3 = 60度 screenWidth / screenHeight:横/縦の画面比 0.1:Near 100:far
perspective(PI / 3, screenWidth / screenHeight, 0.1, 100);
}
let time = 0;
function draw() {
// 背景色を設定
background(200);
// カメラ位置を設定
// camera(eyeX, eyeY, eyeZ, centerX, centerY, centerZ, upX, upY, upZ)
// カメラ位置:(0,0,10), 見る方向:(0,0,0), 上方向:(0,1,0)
camera(0, 0, 5, 0, 0, 0, 0, 1, 0);
// ライティングを設定
ambientLight(100); // 環境光
directionalLight(255, 255, 255, 0.5, 0.5, -1); // 方向光
// 座標系の回転
push();
// 時間を表す変数を進める
time++;
// X軸周りの回転
rotateX(time*0.1);
// Y軸周りの回転
rotateY(time*0.05);
// Z軸周りの回転
rotateZ(time*0.03);
// (red, green, blue)を0~255で色を指定
fill(100, 50, 50);
// 境界線の太さを0.1に指定
strokeWeight(0.1);
// (0,0,0)の位置に(x,y,z)=(2,3,1)の大きさの3Dボックスを描画
box(2, 3, 1);
pop();
}
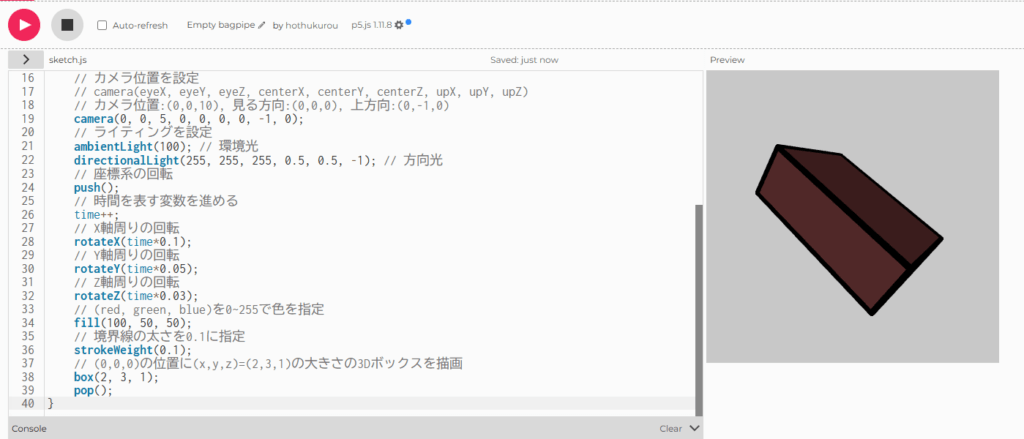
このコードから、Boxを回転させる方法を解説する。
そのために、座標系を回転した後でboxを設置するという動作を行います。
p5.jsでは「boxの座標を指定する」という設置方法ではなく「座標系を移動回転して、その先でboxを設置する」ということで、boxを移動回転しているように見せる。変な指定の仕方に思えるが、意外とよく見る指定方法です。
毎回座標系を変更するのだが、基準座標がずれると座標系がずれていってしまうので、それを防ぐために変更前の座標系をpush関数で保存しておいて、boxの設置が終わったらpop関数で復元することで、元の座標系に戻します。
// 最初の座標系をpushして保存する
push();
// 時間を表す変数を進める
time++;
// X軸周りの回転
rotateX(time*0.1);
// Y軸周りの回転
rotateY(time*0.05);
// Z軸周りの回転
rotateZ(time*0.03);
// (red, green, blue)を0~255で色を指定
fill(100, 50, 50);
// 境界線の太さを0.1に指定
strokeWeight(0.1);
// (0,0,0)の位置に(x,y,z)=(2,3,1)の大きさの3Dボックスを描画
box(2, 3, 1);
// 最初の座標系をpopして復元する
pop();
rotateXはX軸基準で回転する関数。rotateYはY軸基準で回転する関数。rotateZはZ軸基準で回転する関数です。timeという変数はグローバル変数として保持しており、draw関数内で毎回+1していくので、rotateX~Z関数によって、指定される角度は毎回増えていき、この動作によって回転が行われます。
このように座標系の軸に基づいて回転していく時の角度をオイラー角と呼びます。ここからはこのオイラー角による回転を見ていきますが、非常に混乱する話なので、ぜひ左手を以下のような左手座標系に形にしてグルんグルんとまわして確認していきましょう。

オイラー角による回転の解説
まずはrotateXによるX軸周りの回転を見ていこう。
以下のコードをコピペして動作を確認してください。
function setup() {
const screenWidth = 400;
const screenHeight = 400;
// 3Dレンダラーを使用してキャンバスを作成
createCanvas(screenWidth, screenHeight, WEBGL);
// フレームレートを設定
frameRate(30);
// 画角(Field of View)を設定:PI/3 = 60度 screenWidth / screenHeight:横/縦の画面比 0.1:Near 100:Far
perspective(PI / 3, screenWidth / screenHeight, 0.1, 100);
}
let time = 0;
function draw() {
// 背景色を設定
background(200);
// カメラ位置を設定
// camera(eyeX, eyeY, eyeZ, centerX, centerY, centerZ, upX, upY, upZ)
// カメラ位置:(0,0,10), 見る方向:(0,0,0), 上方向:(0,1,0)
camera(0, 0, 5, 0, 0, 0, 0, 1, 0);
// ライティングを設定
ambientLight(100); // 環境光
directionalLight(255, 255, 255, 0.5, 0.5, -1); // 方向光
// 座標系の回転
// 最初の座標系をpushして保存する
push();
// 時間を表す変数を進める
time++;
// X軸周りの回転
rotateX(time*0.1);
// (red, green, blue)を0~255で色を指定
fill(100, 50, 50);
// 境界線の太さを0.1に指定
strokeWeight(0.1);
// (0,0,0)の位置に(x,y,z)=(2,3,1)の大きさの3Dボックスを描画
box(2, 3, 1);
// 最初の座標系をpopして復元する
pop();
}
RotateX(キャンバス横線を軸に回転)
X軸はキャンバスの横方向であるので、この横方向を軸として回転していく。
同じようにY軸回転、Z軸回転を見ていくと以下のようになる。
RotateY(キャンバス縦線を軸に回転)
RotateZ(キャンバス手前方向を軸に回転)
この回転だけならば、左手をグルグル回すことで直感的に理解できるでしょう。
ただ、この回転を複数組み合わせると混乱します。なぜならば、「回転した後の座標系で回転を行う」からです。
ここからは、わかりやすさを重視して、XYZ座標系の軸を回転させてみます。以下コードをコピーして動作を確認しましょう。
function setup() {
const screenWidth = 400;
const screenHeight = 400;
// 3Dレンダラーを使用してキャンバスを作成
createCanvas(screenWidth, screenHeight, WEBGL);
// フレームレートを設定
frameRate(30);
// 画角(Field of View)を設定:PI/3 = 60度 screenWidth / screenHeight:横/縦の画面比 0.1:Near 100:Far
perspective(PI / 3, screenWidth / screenHeight, 0.1, 100);
}
let time = 0;
function draw() {
// 背景色を設定
background(200);
// カメラ位置を設定
// camera(eyeX, eyeY, eyeZ, centerX, centerY, centerZ, upX, upY, upZ)
// カメラ位置:(0,0,10), 見る方向:(0,0,0), 上方向:(0,1,0)
camera(0, 0, 5, 0, 0, 0, 0, 1, 0);
// ライティングを設定
ambientLight(100); // 環境光
directionalLight(255, 255, 255, 0.5, 0.5, -1); // 方向光
// 座標系の回転
// 最初の座標系をpushして保存する
push();
// 時間を表す変数を進める
time++;
// X軸周りの回転
rotateX(time*0.1);
// Y軸周りの回転
rotateY(time*0.05);
// Z軸周りの回転
rotateZ(time*0.03);
drawAxes();
// 最初の座標系をpopして復元する
pop();
}
// XYZ座標軸を描画する関数
function drawAxes() {
strokeWeight(0.3);
// X軸(赤)
stroke(255, 0, 0);
line(0, 0, 0, 3, 0, 0);
// Y軸(緑)- 正方向は下向き
stroke(0, 255, 0);
line(0, 0, 0, 0, 3, 0);
// Z軸(青)
stroke(0, 0, 255);
line(0, 0, 0, 0, 0, 3);
noStroke();
noFill();
}
これは、三次元軸を回転させるためのコードです。
赤:X軸、緑:Y軸、青:Z軸である。
このコードから、以下のX~Z軸回転をコメントアウトして動かないようにしましょう。すると以下のように表示されます。赤いX軸が右向き、緑のY軸が下を向いています。そして、回転指示を与えていないので動かないはずです。
// X軸周りの回転
//rotateX(time*0.1);
// Y軸周りの回転
//rotateY(time*0.05);
// Z軸周りの回転
//rotateZ(time*0.03);

この状態で、X軸に90°回転させてみましょう。ラジアン系で入力するため、Math.PI/2と入力。この動作も、回転量が変わらないため、動かないはずです。
// X軸周りの回転
rotateX(Math.PI/2);
// Y軸周りの回転
//rotateY(time*0.05);
// Z軸周りの回転
//rotateZ(time*0.03);
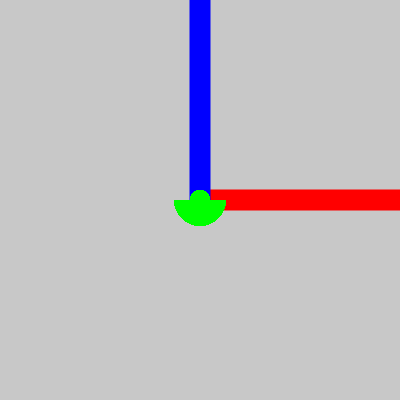
このX軸周りに90°回転させた状態で、以下のようにY軸周りで回転させてみましょう。すると以下のように回っていきます。
// X軸周りの回転
rotateX(Math.PI/2);
// Y軸周りの回転
rotateY(time*0.05);
// Z軸周りの回転
//rotateZ(time*0.03);
この回転の仕方は、X軸を90°回転させた後のY軸を基準として回転しています。
つまり、前回の座標回転をもとにして、次の回転方向が決まります。
これが非常に人間の理解を越えていて混乱するので要注意です。
ちなみにこの時の回転方向は、以下のようにX軸を回転させない時のZ軸周りの回転と同じ動きをします。直前の回転の影響で、軸の回転方向が変わることがわかりますね。
// X軸周りの回転
//rotateX(Math.PI/2);
// Y軸周りの回転
//rotateY(time*0.05);
// Z軸周りの回転
rotateZ(time*0.03);
また、オイラー角による回転は「回転を行う順序で回転する方向が変わる」という点に注意しましょう。
もう一つ具体例を出します。以下のようにX軸周り90°、Y軸周り90°の順番で回転させると以下の図になります。
// X軸周りの回転
rotateX(Math.PI/2);
// Y軸周りの回転
rotateY(Math.PI/2);
// Z軸周りの回転
//rotateZ(time*0.03);
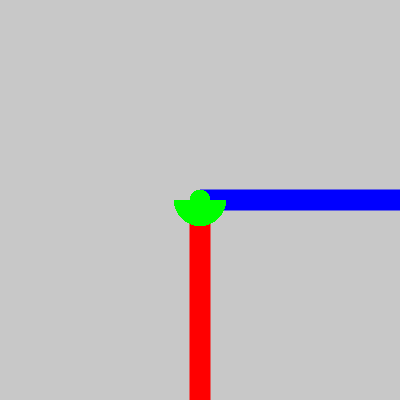
これを順序を変えてY軸周りに90°回転させた後でX軸周りに90°回転させましょう。すると以下のように先ほどとは異なる軸を向くことがわかります。
// Y軸周りの回転
rotateY(Math.PI/2);
// X軸周りの回転
rotateX(Math.PI/2);
// Z軸周りの回転
//rotateZ(time*0.03);
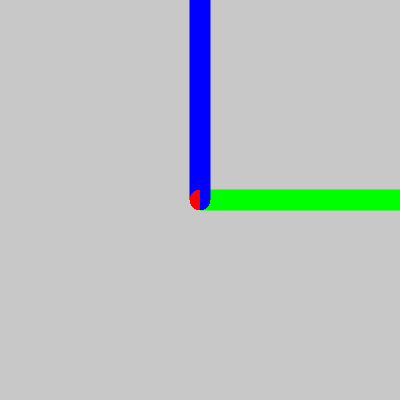
何度も書きますが、オイラー角による回転は「回転を行う順序で回転する方向が変化」します。
このことに注意して、回転方向を決めていきましょう。
オイラー角による姿勢定義
オイラー角による回転はX軸周り、Y軸周り、Z軸周りを決めることによってどのような姿勢でも回転することができます。
この時、1.X軸周り、2.Y軸周り、3.Z軸周りと回転順番を決めることが多いです。この時、XYZ回転と呼んだりします。一度決めさえすれば順番は自由なので、ZYX回転でもYXZ回転でもよく、この3軸全てを回転させるパターンであれば6通りの回転順序の定義があります。ちなみにUnityはZXY回転です。
また、一軸の回転を使わなくても姿勢を定義することができます。例えば、XYX回転、XZX回転、など、1回目と3回目を同じ回転軸にするパターンです。これも6通りあるので、12通りもの回転順序が考えられます。紛らわしいので、3D編集ツールを使ってオイラー角の編集をするときは回転順序の定義を確認することをお勧めします。
ジンバルロックに注意
このような回転順序決定をした時、特定の条件で「どう回転させても目的の姿勢にたどり着けない」という現象が発生することがあります。これをジンバルロックといいます。
原因は「1回目の回転と3回目の回転が同じ回転になり、2回分の回転しか表現できなくなる」ことです。
例えばXYZ回転を考えます。以下はX軸の回転移動とZ軸回転移動を組み合わせていますが、実際に動かすとどちらもZ軸周りの回転をします。これは、1回目のX軸周り回転と3回目のZ軸周りの回転が同じ回転しか表現できないことを示しています。この時回転方向が1軸分減るため、回転できない姿勢が発生してしまいます。
// X軸周りの回転
//rotateX(time*0.03); // X軸は回転しなかった例
// Y軸周りの回転
rotateY(Math.PI/2);
// Z軸周りの回転
rotateZ(time*0.03);
// X軸周りの回転
rotateX(time*0.03); // X軸もかいてんさせた例
// Y軸周りの回転
rotateY(Math.PI/2);
// Z軸周りの回転
rotateZ(time*0.03);
ジンバルロックの発生条件ですが、3軸回転させている時は2軸目が90°、270°回転した時に発生します。
またXYX回転など、一軸目と三軸目が同じ回転軸であるときは2軸目が0°、180°回転した時に発生します。
これは直感的にも同じ回転を1軸目と三軸目がしてしまうことがわかると思います。
移動させてみる
最後に移動をしてみましょう。
function setup() {
const screenWidth = 400;
const screenHeight = 400;
// 3Dレンダラーを使用してキャンバスを作成
createCanvas(screenWidth, screenHeight, WEBGL);
// フレームレートを設定
frameRate(30);
// 画角(Field of View)を設定:PI/3 = 60度 screenWidth / screenHeight:横/縦の画面比 0.1:Near 100:Far
perspective(PI / 3, screenWidth / screenHeight, 0.1, 100);
}
let time = 0;
function draw() {
// 背景色を設定
background(200);
// カメラ位置を設定
// camera(eyeX, eyeY, eyeZ, centerX, centerY, centerZ, upX, upY, upZ)
// カメラ位置:(0,0,10), 見る方向:(0,0,0), 上方向:(0,1,0)
camera(0, 0, 5, 0, 0, 0, 0, 1, 0);
// ライティングを設定
ambientLight(100); // 環境光
directionalLight(255, 255, 255, 0.5, 0.5, -1); // 方向光
// 座標系の回転
// 最初の座標系をpushして保存する
push();
// 時間を表す変数を進める
time++;
// x軸は振動移動しつつ、y=0.5に移動する
translate(Math.cos(time*0.1),0.5,0);
drawAxes();
// 最初の座標系をpopして復元する
pop();
}
// XYZ座標軸を描画する関数
function drawAxes() {
strokeWeight(0.3);
// X軸(赤)
stroke(255, 0, 0);
line(0, 0, 0, 3, 0, 0);
// Y軸(緑)- 正方向は下向き
stroke(0, 255, 0);
line(0, 0, 0, 0, 3, 0);
// Z軸(青)
stroke(0, 0, 255);
line(0, 0, 0, 0, 0, 3);
noStroke();
noFill();
}
translate関数を使うと、指定したxyz座標値に移動できる。
X軸方向に振動移動させたかったので、Math.cos関数を用いた。
// 時間を表す変数を進める
time++;
// x軸は振動移動しつつ、y=0.5に移動する
translate(Math.cos(time*0.1),0.5,0);
また、回転によって座標変換を行ってから移動することで、意図しないような移動を指せることもできる。
// 時間を表す変数を進める
time++;
// X軸周りの回転
//rotateX(time*0.03);
// Y軸周りの回転
//rotateY(Math.PI/2);
// Z軸周りの回転
rotateZ(time*0.03);
// x軸は振動移動しつつ、y=0.5に移動する
translate(Math.cos(time*0.1),0.5,0);
この移動動作も回転順序の前か後かで動作がかわる点に注意する。
もし、先ほどと同じようにX軸のみの振動移動をさせたいときは、先に移動させてから回転させるとよい。先に位置を決めてから姿勢を設定したいパターンの方が多いかと思うので、参考にしてください。
// 時間を表す変数を進める
time++;
// x軸は振動移動しつつ、y=0.5に移動する
translate(Math.cos(time*0.1),0.5,0);
// X軸周りの回転
//rotateX(time*0.03);
// Y軸周りの回転
//rotateY(Math.PI/2);
// Z軸周りの回転
rotateZ(time*0.03);
さいごに
以上でp5.jsを用いた三次元空間に触れあおう講座を終わります。
回転が入ってきたあたりかた脳みそが大混乱を起こしているかと思うのですが、3Dゲーム制作だけでなくロボットアーム操作や3Dスキャナによる三次元計測作業においてもこのような知識を使うことがあると思いますので、もしそのような機会がありましたら参考になりますと幸いです。
そもそもなぜ急にこのような記事を書いたかと言いますと、「p5.jsでWizardry風マップを生成して、ホラーゲーム作れるかな」と検証したことがきっかけでした。
ではまた!