株価データのように、時間が進むにつれ値が連続的に変化していく数列を作りたい時ってありますよね。

今までの値動きから、次の値がある程度予測できるけど、予測が外れることもある、そんな数列の作り方をご紹介します。

具体的にどんな数列がほしいのか

「株価みたいなデータ」と冒頭で説明しましたが、これだとかなりほしいものが曖昧なので、まずはじめに具体的に要件定義をしていきます。

今回の目的は「ゲーム内で使用する、商品の価格を決める数列を作る」ことにしましょう。

また、以下のようなデータがほしいと思っています。

(1)値は0~40の整数値であること。

(2)完全ランダムなデータではなく、前月までの傾向で次月の値がある程度予想できること。

(3)一定周期で上がったり下がったりする。その周期は完全には突き止められないが、ある程度は予想できること。

前月までの値動きでなんとなく次の値が予想できる、そんなデータの作り方を考えていきます。

とりあえず 周期ほしいし sin波か

ここのサブタイトルが575とキレイなリズムになりましたが、それはおいておいて具体的に作ってみましょう。

とりあえず、一定周期のデータを作るためにsin波を生成してみましょう。かんたんにexcelで作成してみます。

sin波の引数に時間tを0,0.4,0.8……と0.4刻みで増やして代入していきます。すると、一定周期で上下する波形が生成できます。

t=2π (6.28……)になると1周期となります。tが0.4刻みで増えていくと、17回目でt=6.4となり1週回ることになりますね。

ちなみにこの0.4のことを次以降ではステップ幅と呼ぶことにします。

これで、-1~1の間を一定周期で変動する数列が生成できました。

ただ、実際には「0~40の値に揃えたい」です。

そのための準備として、「0~1の値に変形してから、その値を40倍する」という変換を入れます。0~1の値に変換するためには、以下の2パターンが考えられます。

(1)平均値を上げて移動するパターン

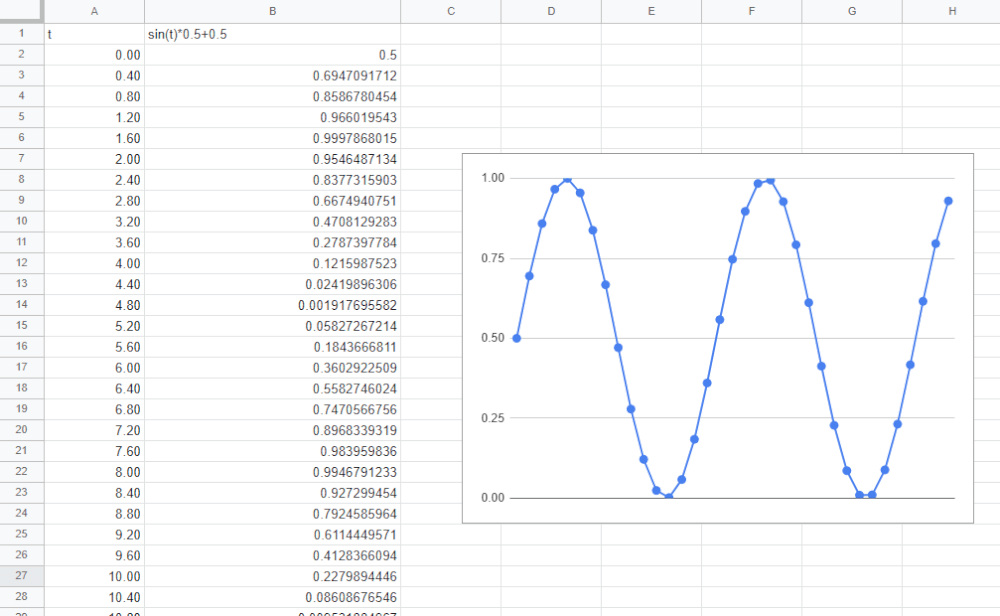
sin(t)を0.5倍しつつ、0.5を加算してあげるパターンです。

こうすると0.5を基準に値が上下してくれます。図をみるとわかりやすいです。

(2)絶対値を取るパターン

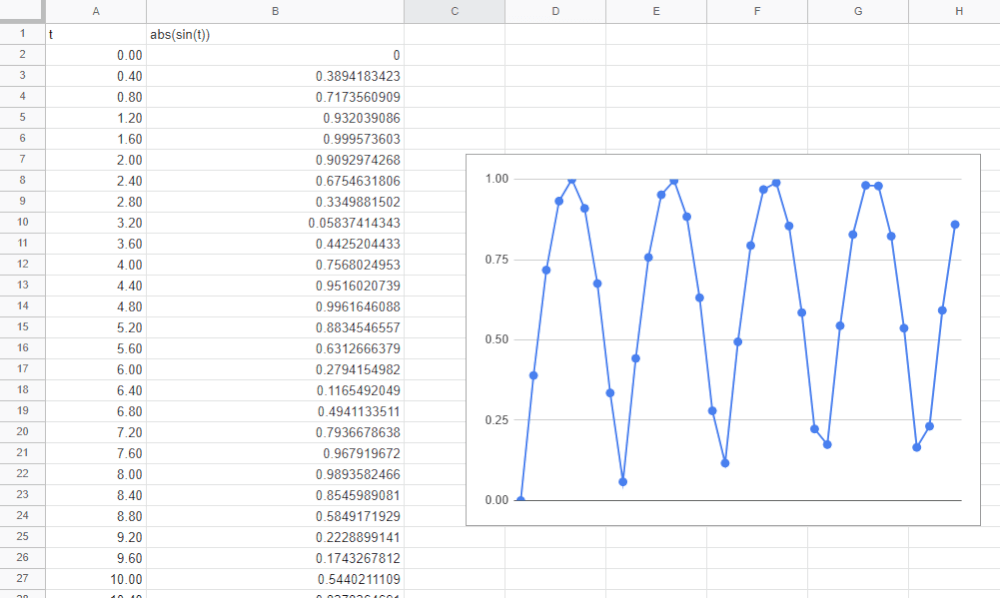
sin(t)の絶対値を取って、マイナスの値をプラスの値にしてしまう方法もあります。

絶対値を取る関数はどんな言語でも、たいていabs()という名前で定義されています。使ってみるとこんな感じの波形になります。

低い値の期間は(1)の平均値を上げるパターンよりも少ない点が主な違いとなります。

どちらを選ぶか

どちらを選ぶかは、目的によるかと思いますが、今回私は(2)の絶対値を取ることにしました。

理由は「ゲームでは値が大きい時にたくさん商品を売って儲けることが主な戦略となる。値が低い期間が長いと、ゲームがだれてしまう恐れがあるため」です。高値期間が大きい方が楽しくなりそうだからですね。

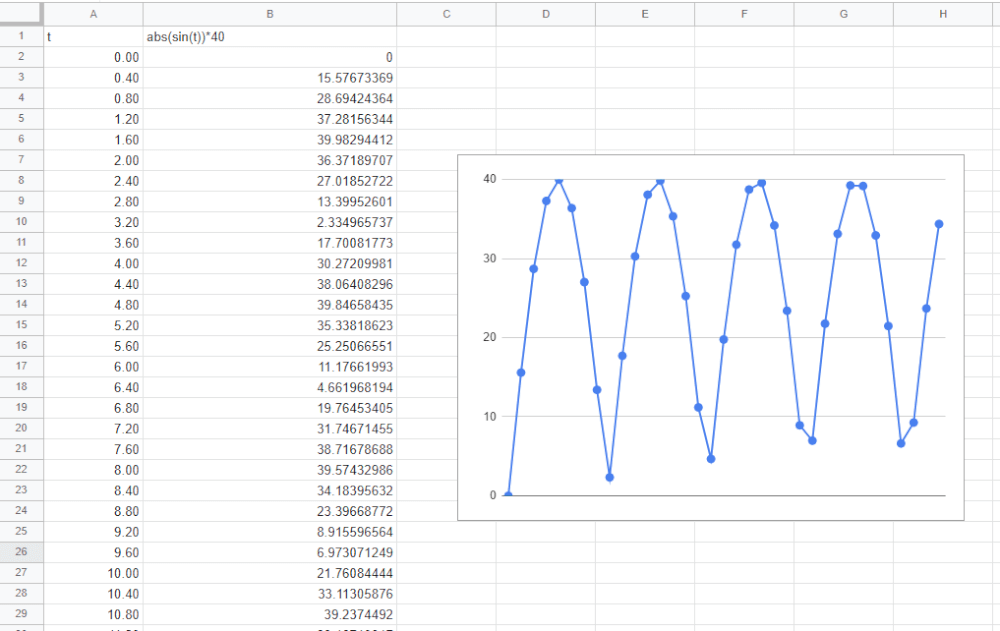
なので、この(2)のパターンを採用して40倍してみました。

これで0~40で値が変動する数列が取れるのですが、さすがにこれでは「値が簡単に予測できてしまう」といった問題が発生します。これは困りものですね。

次からは、この波形にノイズを加えることで、「大まかに予測できるけど、完全に次の値が予測できない数列」を作っていきます。

tのステップ幅をランダムにする

周期のステップ幅を0.4ではなく、0~0.4の間のランダムな値に変換してみるというのが一つの解決策です。

これで、「次上がるのはいつか」というタイミングがわからなくなります。

このランダムな値の作成方法ですが、大抵のプログラミング言語には0~1のランダムな数を生成するrand()関数的なものがあるので、それを用いてrand()*0.4と計算してあげれば、0~0.4の乱数が取り出せますね。

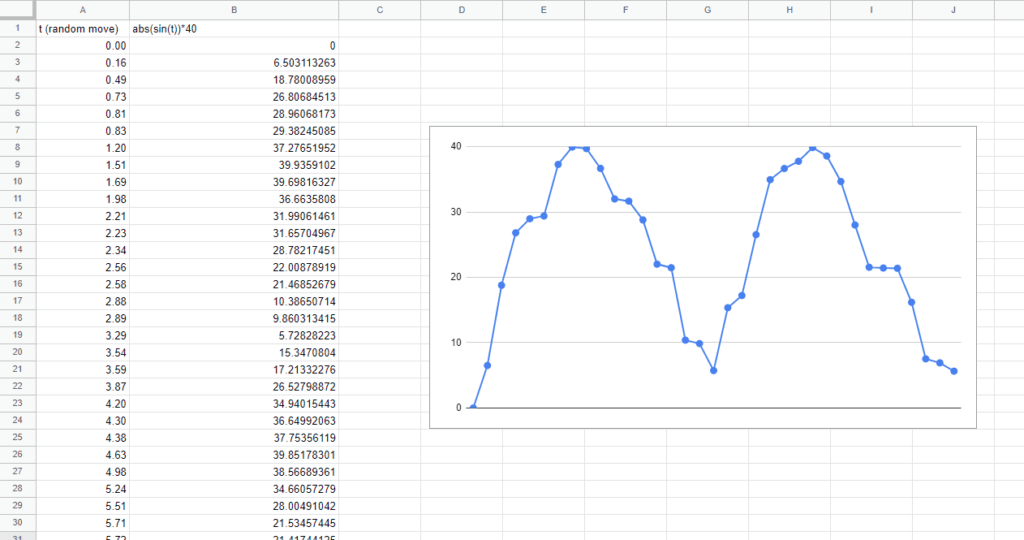
ただ、これだけだと「値が一旦下がりだしたらずっと下がったままになってしまう」など、変動が単調で次の値が予測しやすいという欠点があります。さらなるノイズを加えてみましょう。

ノイズとして二次周期を追加する

ここで次のアイデアとして「メイン周期とは異なる周期で動く二次周期を加算する」ことをします。

具体的には0~30で変動するメインの一次周期と、0~10で変動するサブの二次周期を加算してみると、以下のような波形になりました。２つの波形が最大値のときに30+10=40となるようにしています。

だいぶ乱高下が起きて、「おおまかには次の波形が予測できるけど、完全には予測できない」ような波形になったかと思います。

一次周期の引数t1と二次周期の引数t2は初期値が異なります。初期値を両方とも0にすると、変動幅が似たような形になりやすいので、２つの周期はずらしてあげたほうがノイズ度が高くなります。まあ、このあたりは目的に沿ってカスタマイズできる範囲かなと思います。

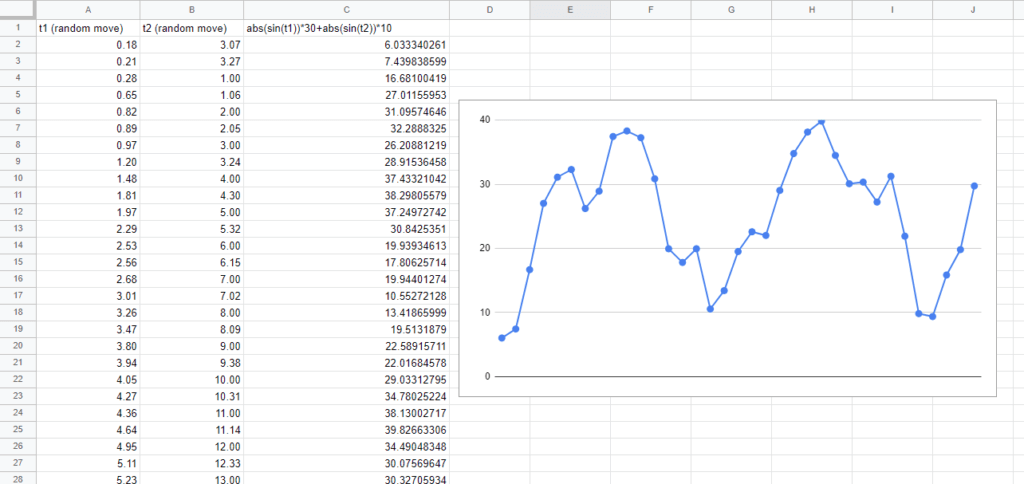
これで、当初欲しかった要件定義をすべて満たすであろう数列の生成に成功しました。

後は、t1とt2のステップ幅を変えてみたり、一次周期と二次周期の変動幅を変えてみたり、三次周期を作成してみたりすると良いかと思います。

まとめ

これにて、「株価みたいに上昇下落がある程度予測できるような数列を生成する方法」の解説を終わります。

今回生成、表示したグラフは以下リンクから閲覧できるので、コピーして値を変更してみるなど、ご自由にお使いください。

https://docs.google.com/spreadsheets/d/1EIrE-q6OP8Vlo8X6A3RDYBfmN3LeMFY0sC_maZq65OI/edit?usp=sharing

また、今回の数列生成を用いたゲームが以下となります。

このゲームでは、あなたがこの世界の創造神となって人類を生成して、誕生Pt.を稼ぐゲームとなります。

この誕生Pt.は今回のような数列によって求められるようになっています。

https://hothukurou.com/game/Factory/index.html

具体的には 誕生ポイント = abs(sin(t1))*25+abs(sin(t2))*10+abs(sin(t3))*5　にて計算しています。

一次周期となるt1のステップ幅は0~0.2とゆっくり目なのですが、ノイズとなる二次三次周期のt2,t3のステップ幅は0~0.8と高めに変動させることで、予測を少しだけ難しくしているのです。

ハイスコアを狙いたい方、グッドエンディングになんとしても到達したい方はぜひこの式を参考に試行錯誤してもらえたら幸いです。